2521: F - Colorful Tree

Memory Limit：128 MB Time Limit：1.000 S
Judge Style：Text Compare Creator：
Submit：3 Solved：2

Description

Problem Statement

There is a tree with N vertices numbered 1 to N. The i-th edge in this tree connects Vertex ai and Vertex bi, and the color and length of that edge are ci and di, respectively. Here the color of each edge is represented by an integer between 1 and N−1 (inclusive). The same integer corresponds to the same color, and different integers correspond to different colors.

Answer the following Q queries:

  • Query j (1≤j≤Q): assuming that the length of every edge whose color is xj is changed to yj, find the distance between Vertex uj and Vertex vj. (The changes of the lengths of edges do not affect the subsequent queries.)

Input


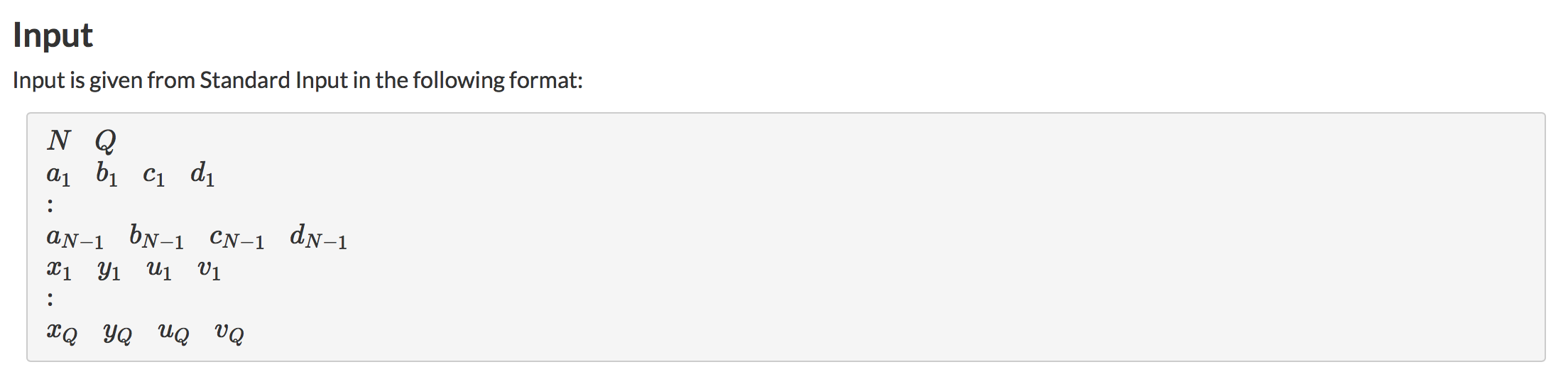
Output

Print Q lines. The j-th line (1≤j≤Q) should contain the answer to Query j.

Sample Input Copy 

5 3
1 2 1 10
1 3 2 20
2 4 4 30
5 2 1 40
1 100 1 4
1 100 1 5
3 1000 3 4

Sample Output Copy 

130
200
60

HINT

The graph in this input is as follows:

Figure

Here the edges of Color 1 are shown as solid red lines, the edge of Color 2 is shown as a bold green line, and the edge of Color 4 is shown as a blue dashed line.

  • Query 1: Assuming that the length of every edge whose color is 1 is changed to 100, the distance between Vertex 1 and Vertex 4 is 100+30=130.
  • Query 2: Assuming that the length of every edge whose color is 1 is changed to 100, the distance between Vertex 1 and Vertex 5 is 100+100=200.
  • Query 3: Assuming that the length of every edge whose color is 3 is changed to 1000 (there is no such edge), the distance between Vertex 3 and Vertex 4is 20+10+30=60. Note that the edges of Color 1 now have their original lengths.

Source/Category

SubmitSubmit RecordStatisticsShowOff!