2077: 【信息学奥赛一本通】方格取数
Memory Limit:128 MB
Time Limit:1.000 S
Judge Style:Text Compare
Creator:
Submit:13
Solved:7
Description
设有N×N的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
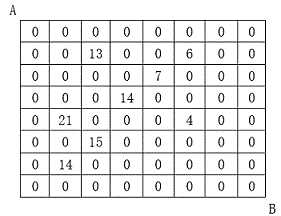
某人从图中的左上角A出发,可以向下行走,也可以向右行走,直到到达右下角的B点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从A点到B点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
Input
第一行为一个整数N(N≤10),表示N×N的方格图。
接下来的每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数。一行“0 0 0”表示结束。
Output
第一个整数,表示两条路径上取得的最大的和。
Sample Input Copy
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0Sample Output Copy
67HINT
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner reader = new Scanner(System.in);
int n = reader.nextInt();
int i = 1, j = 0, k = 0, t = 0;
int[][] a = new int[11][11];
for (int u = 0; u < n; u++) {
for (int v = 0; v < n; v++) {
a[v] = 0;
}
}
while (!(i == 0 && j == 0 && k == 0)) {
i = reader.nextInt();
j = reader.nextInt();
k = reader.nextInt();
a[i][j] = k;
}
int[][][][] b = new int[11][11][11][11];
b[0][0][0][0]=0;
for (i = 1; i <=n; i++) {
for (j = 1; j <=n; j++) {
for (k = 1; k <=n; k++) {
for (t = 1; t <=n; t++) {
b[i][j][k][t] = max(
max(b[i-1][j][k-1][t],
b[i-1][j][k][t-1]),
max(b[i][j-1][k-1][t],
b[i][j-1][k][t-1]));
if (i == k && j == t) {
b[i][j][k][t] += a[i][j];
} else
b[i][j][k][t] += (a[i][j] + a[k][t]);
}
}
}
}
System.out.print(b[n][n][n][n]);
}
private static int max(int a, int b) {
// TODO Auto-generated method stub
int c = a > b ? a : b;
return c;
}
}
————————————————
版权声明:本文为CSDN博主「昨天的光」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_47664976/article/details/117350480
public class Main{
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner reader = new Scanner(System.in);
int n = reader.nextInt();
int i = 1, j = 0, k = 0, t = 0;
int[][] a = new int[11][11];
for (int u = 0; u < n; u++) {
for (int v = 0; v < n; v++) {
a[v] = 0;
}
}
while (!(i == 0 && j == 0 && k == 0)) {
i = reader.nextInt();
j = reader.nextInt();
k = reader.nextInt();
a[i][j] = k;
}
int[][][][] b = new int[11][11][11][11];
b[0][0][0][0]=0;
for (i = 1; i <=n; i++) {
for (j = 1; j <=n; j++) {
for (k = 1; k <=n; k++) {
for (t = 1; t <=n; t++) {
b[i][j][k][t] = max(
max(b[i-1][j][k-1][t],
b[i-1][j][k][t-1]),
max(b[i][j-1][k-1][t],
b[i][j-1][k][t-1]));
if (i == k && j == t) {
b[i][j][k][t] += a[i][j];
} else
b[i][j][k][t] += (a[i][j] + a[k][t]);
}
}
}
}
System.out.print(b[n][n][n][n]);
}
private static int max(int a, int b) {
// TODO Auto-generated method stub
int c = a > b ? a : b;
return c;
}
}
————————————————
版权声明:本文为CSDN博主「昨天的光」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_47664976/article/details/117350480